Stress, Strain and Moduli

Since both of my major projects as well as my coursework are hitting on the subject this week, I though I'd talk about elastic moduli. However, before I can talk about that, we need to talk a bit about stress, strain and the concept of anisotropy.

Stress is fundamentally defined as force per unit area. Strain is the change in length per unit length. In a Cartesian coordinate system (which we use unless we're doing pipes or spheres), this means that to fully describe the stress and strain in three dimension, we end up with matrices.

Stress is typically written as σ, while strain is ε (we use them for conductivity and dielectric constants too...). By combining our two matrices according to the generalized Hooke's Law 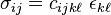, we end up with a fourth-order tensor, Cijkl which we call the stiffness tensor. We can also invert the relationship and get Sijkl which is the compliance tensor. I think every mechanics of materials professor ever wishes the symbols on these two were reversed, but we're stuck with the convention of C=stiffness and S=compliance. 


Now we get to the idea of anisotropy, which is the concept that materials don't behave the same in all orientations. For a perfectly isotropic material (like liquid), the strain response will be the same regardless of direction. In this case, the number of independent elastic constants drops to two: Young's modulus and Poisson's ratio. Young's modulus is also known as the modulus of elasticity, while Poisson's ratio describes the degree to which a materials expands in the unconstrained directions when compressed in the third.  In an anisotropic material, these values are no longer constants, but instead become matrices as well. 


My current research nemesis is the bulk modulus, which is particularly challenging to determine using experiments or simulations. It can either be determined from the derivative of the pressure-volume relationship or the derivative of the pressure-density relationship. In both cases, relaxation and equilibration are critical to minimize scatter in the data. However, reality being what it is, you usually end up with at least some scatter, and can consequently get some crazy derivatives depending on the method you chose for defining the slope at each point.


Bulk modulus is also unique in terms of the anisotropy question: other moduli measure response to a linear stress, be it axial or shear. Bulk modulus describes the compressibility of a material under isotropic pressure, and therefore, the value of the bulk modulus isn't a directional dependent thing. Which is kind of cool. It still makes me want to bang my head on a wall right now, though.